vader 101;&#ENoor moodul,-Idiametraalne inertsi moment varre sektsioonis;-k Initmh – hetke jäikuse koefitsient samaväärse lingi puhul, mis vastab täielikult avatud crack’ile. Võrrand koosneb kahest summast; pragu ja pragu paindlikkusega seotud paindlikkusest ilma pragunemata.See

 tuleb märkida, et olenemata tala kujust, piirtingimustest ja pragu asendist, on valgusvihu üldise paindlikkuse panus sõltub ainult koefitsiendist k Initmm ,st esimene tippkohtumine. Kui kiir pöörleb, muutub pragude osas paindlikkus.Me saame järgmised:vader 101; 

 gil üü&#kiire painduvus ilma praguneta, (kräkist)  q)=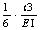 -kmhhetke jäikuse praegune koefitsient antud puhulqJah. -Integrating kaks võrrandid (5) ja (7), saame:vader101;võttes võrrandi (6) arvesse me saame õiguse muuta hetke jäikus sõltuvalt erinevusest etapis

 e q 

 :Võrdse lingi saadud hetkejäikus sõltub ainult šahti läbimõõdust, materjali omadustest ja pragu sügavusest.Crack’i asendi muutus šahtis, šahti omadused, kaasa arvatud tugiüksused, ei muuda samaväärse lingi hetkejäikust (on&#tingimusel, et osa crack jääb sama osa osa osa crack, mille jaoks see olisaadud).Minnes tagasi jäikuse maatriks saadud varem, selle jäikuse koefitsiendid võib kirjutada järgmiselt: vader 

101; k

Init 

 ee , k  Init 

 Ohh hetke jäikuse algväärtused täielikus avatud crack’i vastavate telgede juures&#Jah. Euroopa Liidu kInit ee,kInit  -Ohharvutus võib olla lahendatud kahel viisil.Esimene on hetke jäikuse arvutamine FEM programmis.Teine on see, et kasutada teooria luumurdude mehaanika.See annab võimaluse arvutada avatud cracki kohaliku paindlikkuse koefitsientide väärtusi, kui selle geomeetria, šahti läbimõõt ja materjali omadused on teada [7,10].

 Algoritm rootorisüsteemi simuleerimiseks crack’ iga Tuleks läbida järgmised sammud, et saada koefitsiendid hetke jäikus crack.1. Täielik rootorimudel on loodud ühes eriprogrammidest, mille eesmärk on analüüsida rootoridünaamikat (mille puhulnäiteks Dynamics R4).2. Murdjaga rootori osa on esile tõstetud.  3. Lõhe jagab šahti sektsiooni kaheks allsüsteemiks.Link, mida kirjeldab muutuja maatriksjäikuse koefitsiendid[K (q 

 , 

j)

kuni

mõõde 6x6 asetatakse allsüsteemide vahele.

4. Hetke jäikuse esialgsed koefitsiendid

k

Init

ee ,kInitOhhavatud cracki puhul saadakse antud meetoditegaülal.Need andmed on algandmed.Cracki simuleeriva lingi liitemaatriksi koefitsiendid arvutatakse samal ajal kui integreeritakse liikumise võrrandid 

rootorisüsteemi iga osa kohtaqJah.Mittelineaarse maatriksi võrrandis, mis kirjeldab mittelineaarset dünaamilist mudelitrootorisüsteemi puhul on tegemist järgmisega: vader101;[R ]

– inertsi koefitsientide maatriks;

 [ C ]

_; summutamise ja güroskoopide koefitsientide maatriks;[K

] 

 järgmise põlvkonna maatriks jäikuse koefitsiendid; {Name&#nuõp,{Namenuõp,{Namenuõp_; vastavalt vibreeriva kiirenduse, vibreeriva kiiruse ja vibreeriva nihke kolonnid;{Name-F(m)õp&&mis dünaamiliste koormuste liigid– sisemised ja välised.Samaväärse lingi liitemaatriks võib olla jagatud kaheks osaks: konstant ja muutuja ning vastab tõele järgmine:[&K C] on lisatud üldise jäikuse maatriksi kohta[K]süsteem.Maatriks() [q j] n,Kon kasutatud arvutamiseksmittelineaarse seose reaktsioonid:-vader101; 

 nu RX , 

 nu R– mutual-pöörlemine sektsioonide ümber vastavate telgede.Lõplik liikumise võrrand süsteemi on järgmine:Antud võrrand võib lahendada numbriliste meetoditega, näiteks RungeKutta meetod, Newmark meetod, jne.Soovitatava algoritmi sobivus on tehtud kahe algoritmi paindlikkuse võrdlemiseltugitala koospragu, mis on saadud piiratudelemendi süsteem ja vastavalt dünaamilise R4 eeldatavale algoritmile.Ülesanne on arvutada pragude sektsioonide üksuse jõul langev valgusvihk erinevate faaside jaoks pragu ja jõu vahel.Joonis 3 näitab soovitatud algoritmi kontrollimise tulemusi.Võrreldakse kolme tulemust:paindlikkus arvutatakse piiratud elemendi meetodi (FEM) abil.Tsükli abil töötava kiire mudeli radikaalne paindlikkus arvutatakse FEM-i abil

süsteem, mis hõlmab cracki kogu nurkasendite vahemikku;&#paindlikkus arvutatakse dünaamilise R4 abil, esialgsed andmed saadakse FEM abil.Hetke esialgsed väärtusedtäiesti avatud mõra jäikusk Initee, kInit

Ohhon saadud lahenduse võrrand (7) jaoks

k-Init

mh-ning kiire ja pragu radiaalne paindlikkus

gc-vastava suuna puhul arvutatakse FEM abil.Hetkejäikus vahe- nurkpragude positsioonide puhul muutub minimaalselt maksimumini (10) seaduse kohaselt;

paindlikkus arvutatakse dünaamilise R4 abil.Esialgsed andmed hetkepaindlikkuse kohta täielikult avatud crack’i puhul

-k-ee

 Init , k-Ohh  

Initmis on saadud analüütiliselt kasutades murdmehhaanika algoritme [7, 10].Hetkelise paindlikkuse väärtusvahe- ja nurkmõra positsioonid muutuvad vastavalt seadusele minimaalselt maksimumini (10).Joonis 3 Muutus kiire paindlikkuses crack'i sektsioon pöörde korral FEM-i arvutamisel saadud tulemusedmudel ja mudelid Dynamics R4 on lähedal.Arvutustulemused, mille algtingimused on saadud analüütiliselt, erinevad FEM tulemustest vähem kui 1%.Samal ajal arvutatakse esialgne jäikus analüütiliselt palju kiiremini kui FEM arvutamine ja nõuab vähem töötunde ja nii lihtsamkunikasutamine.  Rotori geomeetria ja parameetrid crack’iga Rotori geomeetria kräkiga on valitud selleks, et näidata algoritmi tööd parimas korras, tabel 1.rootor koos keskse kettaga, toed on paigutatud šahti otstesse.② ②②②

 ② ②-②②②②②②②②②  ② 

②

 ② ② ②-②-②-② 

②

 ② ② ②